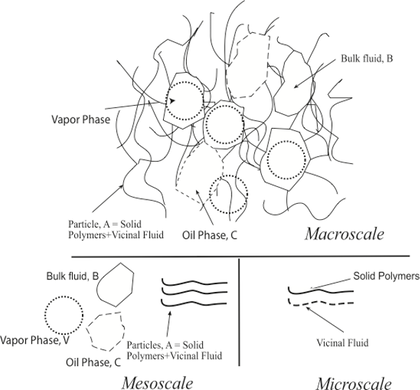
Hybrid mixture theory (HMT) involves using the mathematical filtering theorems to average the microscale field equations to obtain equations at higher scales. At macroscale, the constitutive equations are formulated by exploiting the entropy inequality in the sense of Coleman and Noll (1963). During upscaling (averaging), some microscale information is lost. However, the effect of microscale transport mechanisms and thermomechanical processes on macroscale behavior is incorporated. One significant advantage of upscaling first and then formulating the constitutive theory is that the material coefficients in derived relations appear at the macroscale. The macroscale material coefficients are easier to measure via experiments or obtain from other experimental studies using conventional methods. Upscaled equations are solved in macro and mesoscale representative elementary volumes (REV), which saves the computational time significantly in comparison to time needed for solving the microscale equations.
HMT was initially used to explain the thermomechanical behavior of swelling and shrinking porous media like clays (Hassanizadeh and Gray, 1979; Achanta et al., 1994; Bennethum and Cushman, 1996). Pawan Takhar and coworkers extended the theory for biopolymers for both saturated and unsaturated transport processes (see publications page).
